This report provides a concise summary of one- and two-dimensional (1D and 2D) models for the propagation of linear and nonlinear waves in fractional media, with physical realizations in optics and semi-classical matter waves. The calculus based on the concept of fractional derivatives is a branch of formal mathematics that has been known in the course of 200+ years. Ca. 20 years ago, this concept had appeared in physics in terms of the Laskin’s fractional quantum mechanics, which is based on the one- and multidimensional linear Schrödinger equations with the fractional operator of kinetic energy [1]. These equations are written for the wave function of particles which, in their classical form, move by random Lévy flights. The latter implies that the mean distance $|x|$ of the particle, which moves (in the 1D space) by “flights” from the initial position, $x = 0$, grows with time as $|x|~t^{1/\alpha}$, where $\alpha$ is the Lévy index (LI), which takes values $0 < \alpha \leq 2$. The kinetic-energy operator in the fractional Schrödinger equation is represented by the fractional Riesz derivative, (-\frac{\partial^2}{\partial x^2})^{\alpha/2}, the usual (nonfractional) quantum mechanics corresponding to $\alpha = 2$. While fractional quantum mechanics remains far from experimental implementation, much interest has been drawn to the proposal to emulate the fractional diffraction, governed by the same equations, by means of the classical wave propagation in specially devised optical cavities [2]. This possibility suggests, in turn, to include the self-focusing cubic nonlinearity, as the generic feature of the optical media. In terms of the respective nonlinear fractional Schrödinger equation, many theoretical results have been reported for solitons, vortices and other modes supported by the cubic (or quadratic, alias second-harmonic-generating) optical nonlinearities, see an illustration in the figure, and a brief review of previous results on this topic in [4]. For the solitons, a crucially important issue is their stability. In the 1D model with the cubic or quadratic nonlinearity, the solitons are stable against the onset of the collapse for LI values $1 < \alpha \leq 2$ and $0.5 < \alpha \leq 2$, respectively. In 2D, the cubic self-focusing makes all solitons unstable against the collapse, while the quadratic nonlinearity admits stable solitons for $1 < \alpha \leq 2$. Recently, the first experimental implementation of the effective fractional group-velocity dispersion has been reported for the light propagation in a fiber-laser cavity [5]. This was quickly followed by the first demonstration of fractional solitons in the same setting [6]. An intriguing possibility is to derive a fractional Gross-Pitaevskii (GP) equation for a Bose-Einstein condensate of particles which move by Lévy flights at the classical level, while the usual cubic nonlinearity in this equation represents, in the mean-field (semi-classical) approximation, effects of inter-particle collisions. While the rigorous derivation of the fractional GP equation has not been reported yet, preliminary results have been recently presented, such as stable 1D and 2D solitons produced by the fractional GP equation including the spin-orbit coupling [7].
[1] N. Laskin, Fractional quantum mechanics (World Scientific: Singapore, 2018).
[2] S. Longhi, Opt. Lett. 40, 1117-1120 (2015).
[3] P. Li, H. Sakaguchi, L. Zeng, X. Zhu, D. Mihalache, and B. A. Malomed, Chaos, Solitons & Fractals 173, 113701 (2023).
[4] B. A. Malomed, Photonics 8, 353 (2021); B. A. Malomed, Chaos 34, 022102 (2024).
[5] S. Liu, Y. Zhang, B. A. Malomed, and E. Karimi, Nature Comm. 14, 222 (2023).
[6] S. Liu, Y. Zhang, S. Virally, E. Karimi, B. A. Malomed, and D. V. Seletskiy, Laser & Phot. Reviews 2025, 2401714 (2025).
[7] H. Sakaguchi and B. A. Malomed, J. Phys. B: At. Mol. Opt. Phys. 55, 155301 (2022).

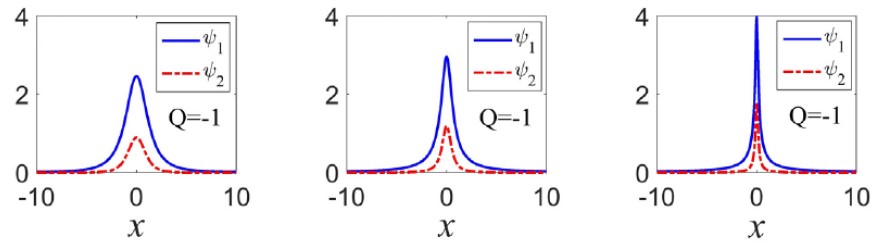
Examples of stable two-component solitons produced in Ref. [3] by the fractional second-harmonic-generating system with mismatch parameter $Q = -1$ and LI values $\alpha = 1.5$ (left), $1.0$ (central), and $0.7$ (right).